First, add #color(red)(6)# to each segment of the system of inequalities to isolate the #t# term while keeping the system balanced:
#-4 + color(red)(6) < 2t - 6 + color(red)(6) < 8 + color(red)(6)#
#2 < 2t - 0 < 14#
#2 < 2t < 14#
Now, divide each segment by #color(red)(2)# to solve for #t# while keeping the system balanced:
#2/color(red)(2) < (2t)/color(red)(2) < 14/color(red)(2)#
#1 < (color(red)(cancel(color(black)(2)))t)/cancel(color(red)(2)) < 7#
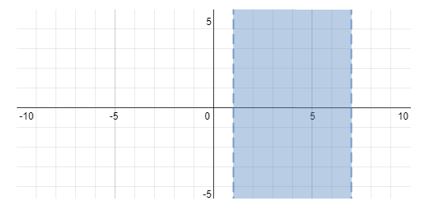
#1 < t < 7#
Or
#t > 1# and #t < 7#
Or, in interval notation:
#(1, 7)#
To graph this we will draw vertical lines at #1# and #7# on the horizontal axis.
The lines will be dashed lines because both inequality operators do not contain an "or equal to" clause.
We will shade between the lines to show the interval: