#" "#
The Compound Inequality Expression given:
#color(red)(5x+10>=10 and 7x-7<=14#
#color(green)("Step 1"#
Consider #5x+10>=10# first and simplify.
Subtract #color(red)(10# to both sides of the inequality to obtain
#5x+10- color(red)(10) >=10 - color(red)(10)#
#5x+cancel 10- color(red)(cancel 10) >=cancel 10 - color(red)(cancel 10)#
#5x>=0#
Divide both sides of the inequality by #color(red)(5)#
#(5x)/color(red)(5)>=0/color(red)(5)#
#(cancel 5x)/color(red)(cancel 5)>=0/color(red)(5)#
#color(blue)(x>=0# Intermediate Solution 1
#color(green)("Step 2"#
Consider #7x-7<=14# next.
Add #color(red)(7)# to both sides of the inequality to get
#7x-7+color(red)(7)<=14+color(red)(7)#
#7x-cancel 7+color(red)(cancel 7)<=14+color(red)(7)#
#7x<=21#
Divide both sides of the inequality by #color(red)(7#
#(7x)/color(red)(7)<=21/color(red)(7#
#(cancel 7x)/color(red)(cancel 7)<=cancel 21^color(red)3/color(red)(cancel 7#
#color(blue)(x<=3# Intermediate Solution 2
#color(green)("Step 3"#
Combine both the Intermediate Solution to obtain:
#color(blue)(x>=0 and color(blue)(x<=3#
#color(red)(0<=x<=3# The required solution
Using the interval notation: #color(red)([0,3]#
#color(green)("Step 4"#
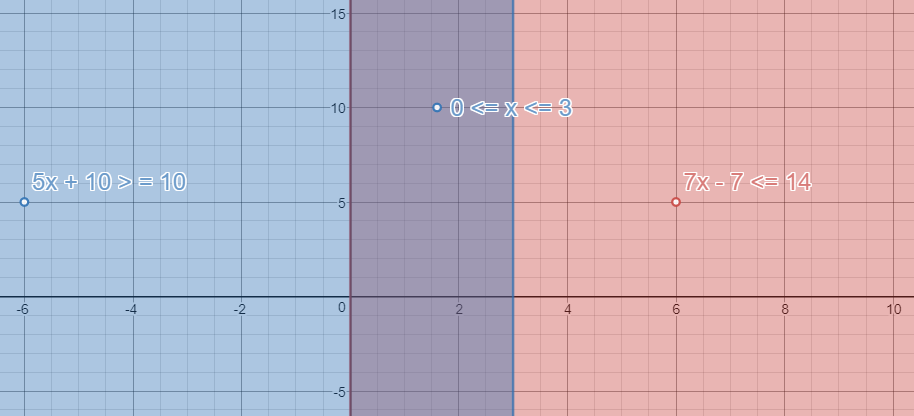
You can verify the results using a graph
The first graph below is created using the two inequality expressions given:
#color(red)(5x+10>=10 and 7x-7<=14#
The solution is the shaded common region
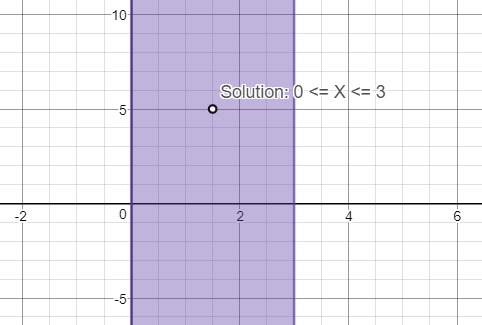
You can also graph just the solution to obtain a solution graph:
#color(red)(0<=x<=3#
Hope you find this solution useful.



