How do you solve the inequality # x + 5 ≥ 2x + 1# and #-4x <-8# ?
1 Answer
Feb 18, 2016
I will solve the first inequality for you and leave the other for you to practice your newfound skill with.
Explanation:
With in equations, always remember that when you multiply or divide by a negative number, you must switch the inequality sign's direction.
Here is the graph of the inequality on a number line.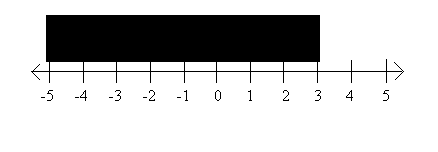
Practice exercises
-
Try your second inequality.
-
Solve and graph the following inequalities.
a)
b)
Good luck!

